A yield curve is a visual display of current conditions in some particular fixed income bond market. It’s a snapshot of interest rates in that market—a simple yet often informative graph that plots yields to maturity on the vertical axis and time to maturity on the horizontal axis for a homogeneous set of securities.
A yield curve also is called the term structure of interest rates. Some academics distinguish the two, preserving one for zero-coupon bonds and the other for standard coupon bonds, but we’ll use them as synonyms and specifically identify the type of securities being discussed.
Yield curves are great for the study of bond math. We can move seamlessly, albeit with some assumptions, between the commonly observed yield curve on coupon bonds and related curves that we derive: the implied spot curve and the implied forward curve. These 2 curves are hugely important in fixed income analysis. It’s no doubt an exaggeration, but we think that the implied forward curve is the single most useful line in fixed income markets, and the implied spot curve is not far behind.
Most yield curves are based on government securities. That’s so we can hold constant all the factors other than time to maturity that impact investors’ required rates of return (in particular, credit risk, liquidity, and taxation). Obviously, all yields should be stated for the same periodicity. This is a problem in practice at the short-term end of the yield curve (i.e., the money market), but it can be rectified with some basic bond math. Also, the yields to maturity ideally would be for zero-coupon securities so that coupon reinvestment risk is not a factor.
In reality, there is no perfect data set for term structure analysis. Typically seen yield curves are plots of street convention yields on coupon-bearing Treasury notes and bonds instead of yields on Treasury STRIPS. In particular, the yields displayed usually are for on-the-run issues (i.e., the most recently auctioned Treasury securities). These are actively traded and typically are priced close to par value, thereby minimizing the effects of the deferral for tax purposes of the gains and losses from buying at a discount or a premium. The problem is that there are gaps in the times to maturity, so some yields have to be interpolated.
Yield to maturity and yield curve shape
The yield to maturity of a bond is the fixed yield such that the sum of the discounted cash flows equals the price of the bond. For different maturity bonds, the yields to maturity will be different. Indeed, instead of discounting by a flat yield, each coupon can be discounted with a zero-coupon bond rate that applies to that maturity.
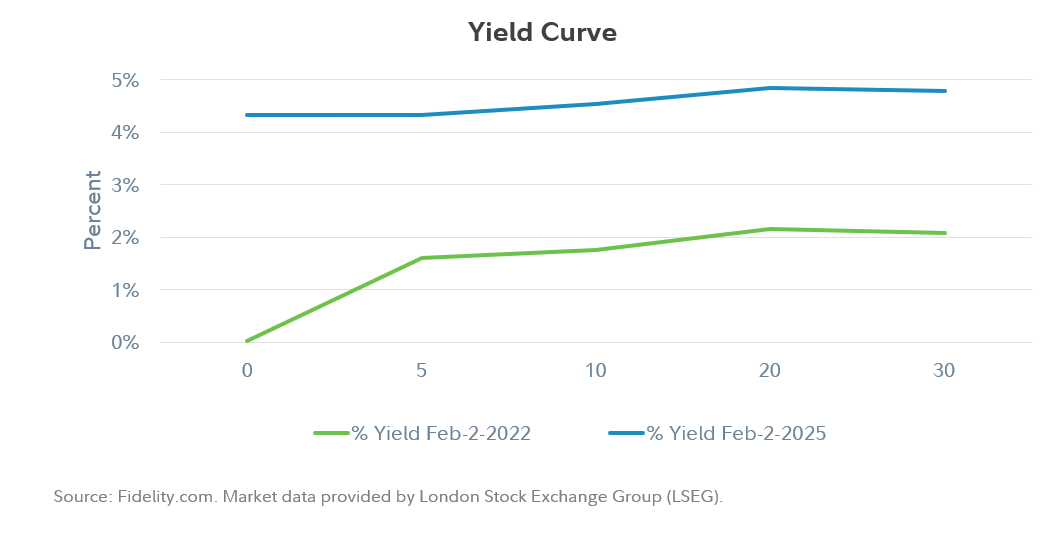
By placing bonds of different maturities on a level playing field, yields can help us see the state of the market at any given time. A simple way to do this is to chart yields of bonds of different maturities with maturity being the x-axis. The example below displays such a graph for February 2, 2022, and for February 2, 2025 to show the variation in the shape over time.
The idea behind the graph is referred to as the yield curve, which more generally can be thought of as the relationship between yields and time to maturity. Mathematically, the yield curve is the set of yields as a function of time; without using mathematical terms, the yield curve can be thought of as a "machine" that takes time to maturity as an input and outputs the yield for a bond of that maturity. The term "yield curve" can also be a source of confusion since the market uses the term "curve" as the slope of yields between 2 maturity points, that is, the difference in yields. These curves are referred to using the two points under consideration, such as 2s/10s curve for the difference between the 10-year and 2-year points. Yield curve trades are discussed specifically later in this chapter, but we will continue to use the general term "yield curve" when referring to the entire set of relationships between yields and time.
Example of 2 different yield curve shapes
Source: Federal Reserve Bank of San Francisco
Why is the yield curve a useful concept? The yield curve can be thought of as the price of lending (borrowing) money over different points in time. For example, the yield curve in the example on February 2, 2022 has an upward slope, which means that investors are willing to lend money at short maturities for very little but will charge a much higher rate to lend money at fixed rates for longer periods of time. Explanations of the shape of the yield curve have tended to be bucketed in 3 broad categories: term premium, expectations, and segmentation.
One reason for the upward slope for February 2, 2022 could be that investors are more comfortable lending out for shorter maturities, such as 1 year, but become increasingly risk-averse for longer periods of time, thus demanding higher yields. This extra yield stemming from risk aversion is known as term premium. Although it may be a contributing factor, term premium alone cannot explain the yield curve since, at times, the yield curve can be downward sloping. Instead, there are likely other factors at work, such as market expectations of yields, more formally known as the "expectations hypothesis." Simply put, the hypothesis attempts to explain the yield curve as market expectations for interest rates in the future.
Looking back at the example, the upward slope in the yield curves may indicate that investors are expecting rates to be higher in the future, which would lead to lending money at low rates for short maturities but at higher rates if the money is locked up for longer maturities. This interpretation of the yield curve can be important for judging the state of the economy and understanding how the yield curve itself may react to changing economic conditions. Finally, the segmentation hypothesis stipulates that certain investor classes prefer to invest in certain maturity ranges, and this segmentation produces the yields we see in the yield curve. Segmentation can be a factor in some parts of the yield curve, such as with pension funds buying longer-end assets to match their long-dated liabilities (e.g., pension payments in the future). However, segmentation is unlikely to be a satisfactory explanation of the yield curve overall—as rates markets have matured, the presence of investors such as hedge funds that are more nimble in their investments and can take advantage of mispricing across the curve makes segmentation unlikely as a major source of yield differences.
In sum, the yield curve is likely a mix of market expectations as well as some risk aversion, while certain niche sectors may feel the effects of segmentation.