Goal
To profit from expected short-term neutral-to-bullish price action in a stock or market index.
Explanation
In return for receiving the premium, the seller of a put assumes the obligation of buying the underlying instrument at the strike price at any time until the expiration date. Although not unlimited, the risk is substantial, because the price of the underlying can fall to zero.
Speculators who sell uncovered puts hope that the price of the underlying stock or market index will trade sideways or rise so that the price of the put will decline. Since stock options in the U.S. typically cover 100 shares, the seller of the put in the example below receives $3.15 per share ($315 less commissions) and assumes the obligation to buy 100 shares of JKL stock at $100 per share until the expiration date (usually the third Friday of the expiration month).
In-the-money options are automatically exercised if they are one cent ($0.01) in the money. Therefore, if an uncovered short put position is open at expiration, it is highly likely that it will be assigned and a long stock position will be created. Uncovered short puts are frequently described as “naked short puts,” because speculators who sell uncovered puts typically do not want a long stock position. As a result, the writers (or speculators) usually close the puts if they are in the money as expiration approaches. Short puts can be closed by entering a “buy to close” order.
Example of short put - uncovered (“naked”)
Sell 1 JKL 100 Put at 3.15
Maximum profit
The potential profit is limited to the premium received less commissions, and this profit is realized if the put is held to expiration and expires worthless.
Maximum risk
Risk is substantial, because the price of the underlying can fall to zero.
Breakeven stock price at expiration
Strike price minus premium received.
In this example: 100.00 − 3.15 = 96.85
Profit/Loss diagram and table: Short 100 Put @ 3.15
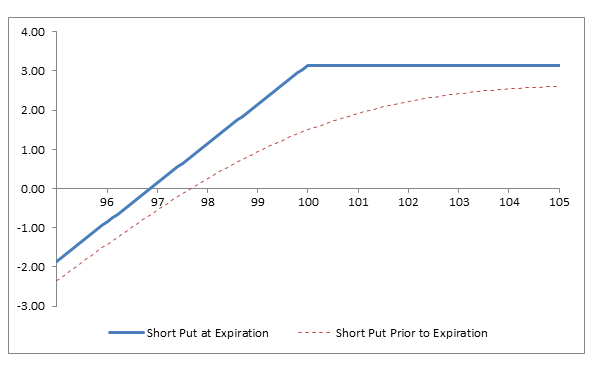
| Stock Price at Expiration | 100 Put Sale Price | 100 Put Value at Expiration | Profit/(Loss) at Expiration |
|---|---|---|---|
| 105 | 3.15 | 0 | +3.15 |
| 104 | 3.15 | 0 | +3.15 |
| 103 | 3.15 | 0 | +3.15 |
| 102 | 3.15 | 0 | +3.15 |
| 101 | 3.15 | 0 | +3.15 |
| 100 | 3.15 | 0 | +3.15 |
| 99 | 3.15 | (1.00) | +2.15 |
| 98 | 3.15 | (2.00) | +1.15 |
| 97 | 3.15 | (3.00) | +0.15 |
| 96 | 3.15 | (4.00) | (0.85) |
| 95 | 3.15 | (5.00) | (1.85) |
Appropriate market forecast
Selling a put uncovered requires a neutral-to-bullish forecast. The forecast must predict that the stock price will not fall below the break-even point before expiration.
Strategy discussion
Selling an uncovered put based on a neutral-to-bullish forecast requires both a high tolerance for risk and trading discipline. A high tolerance for risk is required, because risk is substantial. In practice, a sharp decline in stock price can cause very large losses, losses that could exceed account equity. An unexpected announcement of bad news might cause the underlying stock to gap down in price, which could result in such a loss. Trading discipline is required because the ability to “cut losses short” is an attribute of trading discipline. Many traders who sell uncovered puts have strict guidelines – which they adhere to – about closing positions when the market goes against the forecast.
Impact of stock price change
Put prices, generally, do not change dollar-for-dollar with changes in the price of the underlying stock. Therefore, an investor who sells an uncovered put will typically make or lose less than the owner of 100 shares of stock as the stock price fluctuates.
Put options change in price based on their “delta,” and long put options have negative deltas. Short put option positions, therefore, have positive deltas. At-the-money short puts typically have deltas of approximately +.50, so a $1 rise or fall in stock price causes an at-the-money short put to make or lose approximately 50 cents. In-the-money short puts tend to have deltas between +.50 and +1.00. Out-of-the-money puts tend to have deltas between zero and +.50.
Impact of change in volatility
Volatility is a measure of how much a stock price fluctuates in percentage terms, and volatility is a factor in option prices. As volatility rises, option prices tend to rise if other factors such as stock price and time to expiration remain constant. As a result, short put positions benefit from decreasing volatility and are hurt by rising volatility.
Impact of time
The time value portion of an option’s total price decreases as expiration approaches. This is known as time erosion. Short puts benefit from passing time if other factors remain constant.
Risk of early assignment
Stock options in the United States can be exercised on any business day, and the holder of a short option position has no control over when they will be required to fulfill the obligation. Therefore, the risk of early assignment is a real risk that must be considered.
Sellers of uncovered puts must consider the risk of early assignment and should be aware of when the risk is greatest. Early assignment of stock options is generally related to dividends, and short puts that are assigned early are generally assigned on the ex-dividend date. In-the-money short puts whose time value is less than the dividend have a high likelihood of being assigned.
Potential position created at expiration
If a put is assigned, then stock is purchased at the strike price of the put. In the case of an uncovered put where there is no offsetting short stock position, a long stock position is created. Since options are automatically exercised at expiration if they are one cent ($0.01) in the money, if a seller of an uncovered put wants to avoid having a long stock position when a put is in the money, the short put must be closed prior to expiration.
Other considerations
Speculators who sell uncovered puts generally do not want a long position in the underlying stock. It is therefore necessary for such speculators to watch uncovered short put positions closely and to close a position if the market moves against the neutral-to-bullish forecast. A short put position can be closed by entering a buy to close order.
