Potential goals
To profit from a large stock price move away from the strike price of the calendar spread with limited risk if there is little or no price change.
Explanation
A short calendar spread with puts is created by selling one “longer-term” put and buying one “shorter-term” put with the same strike price. In the example a two-month (56 days to expiration) 100 Put is sold and a one-month (28 days to expiration) 100 Put is purchased. This strategy is established for a net credit (net receipt), and both the profit potential and risk are limited. The maximum profit is realized if the stock price is far above or far below to the strike price on the expiration date of the long put, and the maximum risk is realized if the stock price is at the strike price.
Example of short calendar spread with puts
| Buy 1 28-day XYZ 100 put | (3.25) |
| Sell 1 56-day XYZ 100 put | 4.60 |
| Net credit = | 1.35 |
Maximum profit
The maximum profit potential of a short calendar spread with puts is the net credit received less commissions. This profit is realized if the stock price is either far above or far below the strike price of the calendar spread at expiration of the long put. Whether the stock price rises or falls, if it moves sharply away from the strike price, then the difference between the two puts approaches zero and the full amount received for the spread is kept as income. For example, if the stock price falls sharply so that both puts are deep in the money, then the prices of both puts approach parity for a net difference of zero. If the stock price rises sharply so that both puts are far out of the money, then the price of both puts approach zero for a net difference of zero.
Maximum risk
The potential maximum risk of a short calendar spread with puts is substantial if the long put expires worthless and short put (with a later expiration date) remains open. It is therefore essential to monitor a short calendar spread position as the expiration date of the long put approaches.
Assuming that the long put is open, the maximum risk of a short calendar spread with puts occurs if the stock price equals the strike price of the puts on the expiration date of the long put (shorter term). This is the point of maximum loss, because the short put (longer term) has maximum time value when the stock price equals the strike price. Also, since the long put expires worthless when the stock price equals the strike price at expiration, the difference in price between the two puts is at its greatest.
It is impossible to know for sure what the maximum loss will be, because the maximum loss depends of the price of short put which can vary based on the level of volatility.
Breakeven stock price at expiration of the long put
Conceptually, there are two breakeven points, one above the strike price of the calendar spread and one below. Also, conceptually, the breakeven points are the stock prices on the expiration date of the long put at which the time value of the short put equals the original price of the calendar spread. However, since the time value of the short put depends on the level of volatility, it is impossible to know for sure what the breakeven stock prices will be.
Profit/Loss diagram and table: short calendar spread with puts
| Buy 1 28-day XYZ 100 Put | at | (3.25) |
| Sell 1 56-day XYZ 100 Put | at | 4.60 |
| Net Credit | = | 1.35 |
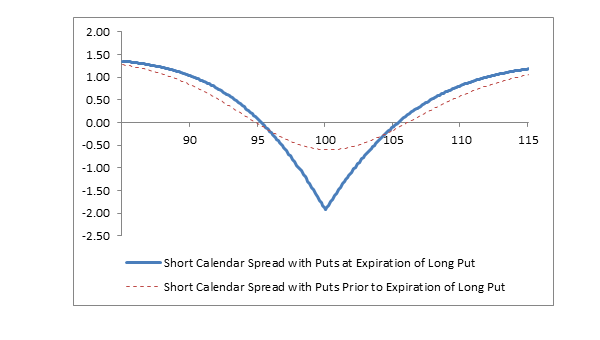
| Stock Price at Expiration of the 28-day Put | Long 1 28-day 100 Put Profit/(Loss) at Expiration | Short 1 56-day 100 Put Profit/(Loss) at Expiration of the 28-day Put* | Net Profit/(Loss) at Expiration of the 28-day Put |
|---|---|---|---|
| 115 | (3.25) | +4.45 | +1.20 |
| 110 | (3.25) | +4.05 | +0.80 |
| 105 | (3.25) | +3.15 | (0.10) |
| 100 | (3.25) | +1.35 | (1.90) |
| 95 | +1.75 | (1.65) | +0.10 |
| 90 | +6.75 | (5.70) | +1.05 |
| 85 | +11.75 | (10.40) | +1.35 |
*Profit or loss of the short put is based on its estimated value on the expiration date of the long put. This value was calculated using a standard Black-Scholes options pricing formula with the following assumptions: 28 days to expiration, volatility of 30%, interest rate of 1% and no dividend.
Appropriate market forecast
A short calendar spread with puts realizes its maximum profit if the stock price is either far above or far below the strike price on the expiration date of the long put. The ideal forecast, therefore, is for a “big stock price change when the direction of the change could be either up or down.” In the language of options, this is known as “high volatility.”
Strategy discussion
A short calendar spread with puts is a possible strategy choice when the forecast is for a big stock price change but the direction of the change is uncertain. Short calendar spreads with puts are often established before earnings reports, before new product introductions and before FDA announcements. These are typical of situations in which “good news” could send a stock price sharply higher, or “bad news” could send a stock price sharply lower. The risk is that the announcement does not cause a significant change in stock price and, as a result, the price of the short calendar spread increases and a loss is incurred.
It is important to remember that the prices of options – and therefore the prices of calendar spreads – contain the consensus opinion of options market participants as to how much the stock price will move prior to expiration. This means that sellers of calendar spreads believe that the market consensus is “too low” and that the stock price will move beyond a breakeven point – either up or down.
The same logic applies to options prices before earnings reports and other such announcements. Dates of announcements of important information are generally publicized in advanced and are well-known in the marketplace. Furthermore, such announcements are likely, but not guaranteed, to cause the stock price to change dramatically. As a result, prices of calls, puts and calendar spreads adjust prior to such announcements. In the language of options, this is known as an “increase in implied volatility.”
An increase in implied volatility increases the risk of trading options. For sellers of calendar spreads, higher implied volatility means that breakeven points are farther apart and that the underlying stock price has to move further to achieve breakeven.
“Selling a calendar spread” is intuitively appealing, because “you can make money if the stock price rises or falls.” The reality is that the market is often “efficient,” which means that prices of calendar spreads frequently are an accurate gauge of how much a stock price is likely to move prior to expiration. This means that selling a calendar spread, like all trading decisions, is subjective and requires good timing for both the position entry decision and the exit decision.
Impact of stock price change
“Delta” estimates how much a position will change in price as the stock price changes. Long puts have negative deltas, and short puts have positive deltas. The net delta of a short calendar spread with puts is usually close to zero, but, as expiration approaches, it varies from −0.50 to +0.50 depending on the relationship of the stock price to the strike price of the spread.
With approximately 20 days to expiration of the short put, the net delta varies from approximately +0.10 with the stock price 5% below the strike price to −0.10 with the stock price 5% above the strike price.
With approximately 10 days to expiration of the short put, the net delta varies from approximately +0.20 with the stock price 5% below the strike price to −0.20 with the stock price 5% above the strike price.
When the stock price is slightly below the strike price as expiration approaches, the position delta approaches −0.50, because the delta of the short put is approximately +0.50 and the delta of the long put approaches −1.00.
When the stock price is slightly above the strike price as expiration approaches, the position delta approaches +0.50, because the delta of the short put is approximately +0.50 and the delta of the long put approaches 0.00.
The position delta approaches 0.00 if the puts are deep in the money (stock price below strike price) or far out of the money (stock price above strike price). If the puts are deep in the money, then the delta of the short put approaches +1.00 and the delta of the long put approaches −1.00 for a net spread delta of 0.00. If the puts are out of the money, then the deltas of both puts approach 0.00.
Impact of change in volatility
Volatility is a measure of how much a stock price fluctuates in percentage terms, and volatility is a factor in option prices. As volatility rises, option prices tend to rise if other factors such as stock price and time to expiration remain constant. Long options, therefore, rise in price and make money when volatility rises, and short options rise in price and lose money when volatility rises. When volatility falls, the opposite happens; long options lose money and short options make money. “Vega” is a measure of how much changing volatility affects the net price of a position.
Since a short calendar spread with puts has one short put with more time to expiration and one long put with the same strike price and less time, the impact of changing volatility is slightly negative, but very close to zero. The net vega is slightly negative, because the vega of the short put is slightly greater than the vega of the long put. As expiration approaches, the net vega of the spread approaches the vega of the short put, because the vega of the long put approaches zero.
Impact of time
The time value portion of an option’s total price decreases as expiration approaches. This is known as time erosion. “Theta” is a measure of how much time erosion affects the net price of a position. Long option positions have negative theta, which means they lose money from time erosion, if other factors remain constant; and short options have positive theta, which means they make money from time erosion.
Since a short calendar spread with puts has one short put with more time to expiration and one long put with the same strike price and less time, the impact of time erosion is negative if the stock price is near the strike price of the puts. In the language of options, this is a “net negative theta.” Furthermore, the negative impact of time erosion increases as expiration approaches, because the value of the short-term long at-the-money put decays at an increasing rate.
If the stock price rises above or falls below the strike price of the calendar spread, however, the impact of time erosion becomes slightly positive. In either of these cases, the time value of the shorter-term long put approaches zero, but the time value of the longer-term short put remains positive and decreases with passing time.
Risk of early assignment
Stock options in the United States can be exercised on any business day, and holders of short stock option positions have no control over when they will be required to fulfill the obligation. Therefore, the risk of early assignment is a real risk that must be considered when entering into positions involving short options.
While the long put in a short calendar spread with puts has no risk of early assignment, the short put does have such risk. Early assignment of stock options is generally related to dividends, and short puts that are assigned early are generally assigned on the ex-dividend date. In-the-money puts whose time value is less than the dividend have a high likelihood of being assigned.
If assignment is deemed likely and if a long stock position is not wanted, then appropriate action must be taken. Before assignment occurs, the risk of assignment can be eliminated in two ways. First, the entire spread can be closed by selling the long put to close and buying the short put to close. Alternatively, the short put can be purchased to close and the long put can be kept open.
If early assignment of the short put does occur, stock is purchased, and a long stock position is created. If a long stock position is not wanted, there are two choices. First, the long stock can be sold by exercising the long put. Second, shares can be sold in the marketplace and the long put can be left open. Generally, if there is time value in the long put, then it is preferable to sell the shares and sell the long put rather than exercise it. It is preferable to sell shares in this case, because the time value will be lost if the long put is exercised. Also, generally, if the longer-term short put in a short calendar spread is assigned early, then there is little or no time value in the shorter-term long put. In this case it is usually preferable to sell the unwanted long shares by exercising the long put. Such action then closes the entire position and frees up capital for other uses.
Note, also, that whichever method is used to close the long stock position, the date of the stock sale will be one day later than the date of the purchase. This difference will result in additional fees, including interest charges and commissions. Assignment of a short put might also trigger a margin put if there is not sufficient account equity to support the long stock position.
Potential position created at expiration of the short put
If the short put is assigned after the long put expires, then stock is purchased and a straight long stock position is created and the potential risk is substantial.
However, if the short put is assigned prior to expiration of the long put, then stock is purchased and the result is a two-part position consisting of long stock and long put. This position has limited risk on the downside and substantial profit potential on the upside. If a trader has a bullish forecast, then this position can be maintained in hopes that the forecast will be realized and a profit earned. If the long stock position is not wanted, then the position must be closed either by exercising the put or by sell stock and selling the put (see Risk of Early Assignment above).
Other considerations
Short calendar spreads with puts are frequently compared to long straddles and long strangles, because all three strategies profit from “high volatility” in the underlying stock. The differences between the three strategies are the initial cost, the risk and the profit potential. In dollar terms, straddles and strangles cost much more to establish, have greater, albeit limited, risk and have unlimited profit potential. Short calendar spreads, in contrast, require less capital (margin requirement) to establish, have a smaller limited risk and have limited profit potential. One should not conclude, however, that traders with limited capital should prefer short calendar spreads to long straddles or long strangles. The risk of a short calendar spread is still 100% of the capital committed. The decision to trade any strategy involves choosing an amount of capital that will be placed at risk and potentially lost if the market forecast is not realized. In this regard, choosing a short calendar spread is similar to choosing any strategy.
The short calendar spread with puts is also known by two other names, a “short time spread” and a “short horizontal spread.” “Short” in the strategy name implies that the strategy is established for a net credit, or net receipt of cash. The terms “time” and “horizontal” describe the relationship between the expiration dates. “Time” implies that the options expire at different times, or on different dates. The term “horizontal” originated when options prices were listed in newspapers in a tabular format. Strike prices were listed vertically, and expirations were listed horizontally. Therefore a “horizontal spread” involved options in the same row of the table; they had the same strike price but they had different expiration dates.
