Goal
To profit from a big price change – either up or down – in the underlying stock.
A long straddle consists of one long call and one long put. Both options have the same underlying stock, the same strike price and the same expiration date. A long straddle is established for a net debit (or net cost) and profits if the underlying stock rises above the upper break-even point or falls below the lower break-even point. Profit potential is unlimited on the upside and substantial on the downside. Potential loss is limited to the total cost of the straddle plus commissions.
Example of long straddle
| Buy 1 XYZ 100 call at | (3.30) |
| Buy 1 XYZ 100 put at | (3.20) |
| Net cost = | (6.50) |
Profit potential is unlimited on the upside, because the stock price can rise indefinitely. On the downside, profit potential is substantial, because the stock price can fall to zero.
Potential loss is limited to the total cost of the straddle plus commissions, and a loss of this amount is realized if the position is held to expiration and both options expire worthless. Both options will expire worthless if the stock price is exactly equal to the strike price at expiration.
There are two potential break-even points:
- Strike price plus total premium: In this example: 100.00 + 6.50 = 106.50
- Strike price minus total premium: In this example: 100.00 – 6.50 = 93.50
| Long 1 100 call at | (3.30) |
| Long 1 100 put at | (3.20) |
| Net cost = | (6.50) |
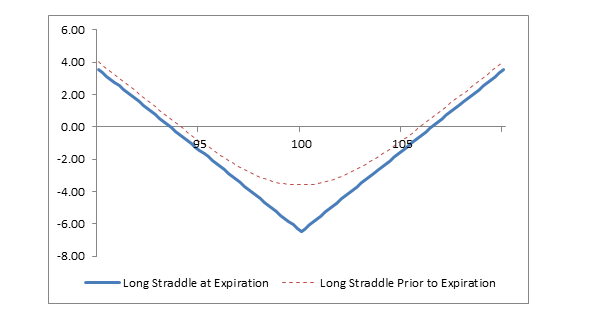
| Stock Price at Expiration | Long 100 Call Profit/(Loss) at Expiration | Long 100 Put Profit/(Loss) at Expiration | Long Straddle Profit / (Loss) at Expiration |
|---|---|---|---|
| 110 | +6.70 | (3.20) | +3.50 |
| 109 | +5.70 | (3.20) | +2.50 |
| 108 | +4.70 | (3.20) | +1.50 |
| 107 | +3.70 | (3.20) | +0.50 |
| 106 | +2.70 | (3.20) | (0.50) |
| 105 | +1.70 | (3.20) | (1.50) |
| 104 | +0.70 | (3.20) | (2.50) |
| 103 | (0.30) | (3.20) | (3.50) |
| 102 | (1.30) | (3.20) | (4.50) |
| 101 | (2.30) | (3.20) | (5.50) |
| 100 | (3.30) | (3.20) | (6.50) |
| 99 | (3.30) | (2.20) | (5.50) |
| 98 | (3.30) | (1.20) | (4.50) |
| 97 | (3.30) | (0.20) | (3.50) |
| 96 | (3.30) | +0.80 | (2.50) |
| 95 | (3.30) | +1.80 | (1.50) |
| 94 | (3.30) | +2.80 | (0.50) |
| 93 | (3.30) | +3.80 | +0.50 |
| 92 | (3.30) | +4.80 | +1.50 |
| 91 | (3.30) | +5.80 | +2.50 |
| 90 | (3.30) | +6.80 | +3.50 |
A long straddle profits when the price of the underlying stock rises above the upper breakeven point or falls below the lower breakeven point. The ideal forecast, therefore, is for a “big stock price change when the direction of the change could be either up or down.” In the language of options, this is known as “high volatility.”
A long – or purchased – straddle is the strategy of choice when the forecast is for a big stock price change but the direction of the change is uncertain. Straddles are often purchased before earnings reports, before new product introductions and before FDA announcements. These are typical of situations in which “good news” could send a stock price sharply higher, or “bad news” could send a stock price sharply lower. The risk is that the announcement does not cause a significant change in stock price and, as a result, both the call price and put price decrease as traders sell both options.
It is important to remember that the prices of calls and puts – and therefore the prices of straddles – contain the consensus opinion of options market participants as to how much the stock price will move prior to expiration. This means that buyers of straddles believe that the market consensus is “too low” and that the stock price will move beyond a breakeven point – either up or down.
The same logic applies to options prices before earnings reports and other such announcements. Dates of announcements of important information are generally publicized in advance and well-known in the marketplace. Furthermore, such announcements are likely, but not guaranteed, to cause the stock price to change dramatically. As a result, prices of calls, puts and straddles frequently rise prior to such announcements. In the language of options, this is known as an “increase in implied volatility.”
An increase in implied volatility increases the risk of trading options. Buyers of options have to pay higher prices and therefore risk more. For buyers of straddles, higher options prices mean that breakeven points are farther apart and that the underlying stock price has to move further to achieve breakeven. Sellers of straddles also face increased risk, because higher volatility means that there is a greater probability of a big stock price change and, therefore, a greater probability that an option seller will incur a loss.
“Buying a straddle” is intuitively appealing, because “you can make money if the stock price moves up or down.” The reality is that the market is often “efficient,” which means that prices of straddles frequently are an accurate gauge of how much a stock price is likely to move prior to expiration. This means that buying a straddle, like all trading decisions, is subjective and requires good timing for both the buy decision and the sell decision.
When the stock price is at or near the strike price of the straddle, the positive delta of the call and negative delta of the put very nearly offset each other. Thus, for small changes in stock price near the strike price, the price of a straddle does not change very much. This means that a straddle has a “near-zero delta.” Delta estimates how much an option price will change as the stock price changes.
However, if the stock price “rises fast enough” or “falls fast enough,” then the straddle rises in price. This happens because, as the stock price rises, the call rises in price more than the put falls in price. Also, as the stock price falls, the put rises in price more than the call falls. In the language of options, this is known as “positive gamma.” Gamma estimates how much the delta of a position changes as the stock price changes. Positive gamma means that the delta of a position changes in the same direction as the change in price of the underlying stock. As the stock price rises, the net delta of a straddle becomes more and more positive, because the delta of the long call becomes more and more positive and the delta of the put goes to zero. Similarly, as the stock price falls, the net delta of a straddle becomes more and more negative, because the delta of the long put becomes more and more negative and the delta of the call goes to zero.
Volatility is a measure of how much a stock price fluctuates in percentage terms, and volatility is a factor in option prices. As volatility rises, option prices – and straddle prices – tend to rise if other factors such as stock price and time to expiration remain constant. Therefore, when volatility increases, long straddles increase in price and make money. When volatility falls, long straddles decrease in price and lose money. In the language of options, this is known as “positive vega.” Vega estimates how much an option price changes as the level of volatility changes and other factors are unchanged, and positive vega means that a position profits when volatility rises and loses when volatility falls.
The time value portion of an option’s total price decreases as expiration approaches. This is known as time erosion, or time decay. Since long straddles consist of two long options, the sensitivity to time erosion is higher than for single-option positions. Long straddles tend to lose money rapidly as time passes and the stock price does not change.
Owners of options have control over when an option is exercised. Since a long straddle consists of one long, or owned, call and one long put, there is no risk of early assignment.
There are three possible outcomes at expiration. The stock price can be at the strike price of a long straddle, above it or below it.
If the stock price is at the strike price of a long straddle at expiration, then both the call and the put expire worthless and no stock position is created.
If the stock price is above the strike price at expiration, the put expires worthless, the long call is exercised, stock is purchased at the strike price and a long stock position is created. If a long stock position is not wanted, the call must be sold prior to expiration.
If the stock price is below the strike price at expiration, the call expires worthless, the long put is exercised, stock is sold at the strike price and a short stock position is created. If a short stock position is not wanted, the put must be sold prior to expiration.
Note: options are automatically exercised at expiration if they are one cent ($0.01) in the money. Therefore, if the stock price is “close” to the strike price as expiration approaches, and if the owner of a straddle wants to avoid having either a long or short stock position, the long straddle must be sold prior to expiration.
Long straddles are often compared to long strangles, and traders frequently debate which is the “better” strategy.
Long straddles involve buying a call and put with the same strike price. For example, buy a 100 Call and buy a 100 Put. Long strangles, however, involve buying a call with a higher strike price and buying a put with a lower strike price. For example, buy a 105 Call and buy a 95 Put.
Neither strategy is “better” in an absolute sense. There are tradeoffs.
There are three advantages and two disadvantages of a long straddle. The first advantage is that the breakeven points are closer together for a straddle than for a comparable strangle. Second, there is less of a chance of losing 100% of the cost of a straddle if it is held to expiration. Third, long straddles are less sensitive to time decay than long strangles. Thus, when there is little or no stock price movement, a long straddle will experience a lower percentage loss over a given time period than a comparable strangle. The first disadvantage of a long straddle is that the cost and maximum risk of one straddle (one call and one put) are greater than for one strangle. Second, for a given amount of capital, fewer straddles can be purchased.
The long strangle has two advantages and three disadvantages. The first advantage is that the cost and maximum risk of one strangle are lower than for one straddle. Second, for a given amount of capital, more strangles can be purchased. The first disadvantage is that the breakeven points for a strangle are further apart than for a comparable straddle. Second, there is a greater chance of losing 100% of the cost of a strangle if it is held to expiration. Third, long strangles are more sensitive to time decay than long straddles. Thus, when there is little or no stock price movement, a long strangle will experience a greater percentage loss over a given time period than a comparable straddle.
