Potential goal
To profit from neutral stock price action between the strike prices of the short calls with limited risk.
Explanation
A double diagonal spread is created by buying one “longer-term” straddle and selling one “shorter-term” strangle. In the example below, a two-month (56 days to expiration) 100 Straddle is purchased and a one-month (28 days to expiration) 95 – 105 Strangle is sold. This strategy is established for a net debit, and both the profit potential and risk are limited. The maximum profit is realized if the stock price is equal to the strike price of one of the short options on the expiration date of the short-term options, and the maximum risk is realized if the stock price is equal to the strike price of the straddle and if the straddle is held to its expiration.
This is an advanced strategy because the profit potential is small in dollar terms. As a result, it is essential to open and close the position at “good prices.”
Example of double diagonal spread
| Sell 1 28-day XYZ 95 put at | 1.30 |
| Buy 1 56-day XYZ 100 put at | (3.80) |
| Buy 1 56-day XYZ 100 call at | (4.00) |
| Sell 1 28-day XYZ 105 call at | 1.50 |
| Net cost = | (5.00) |
Maximum profit
The maximum profit is realized if the stock price is equal to one of the strike prices of the short strangle on the expiration date of the short strangle. With the stock price at the strike price of the short call at expiration of the strangle, for example, the profit equals the price of the long straddle minus the net cost of the diagonal spread including commissions. This is a point of maximum profit because the long call component of the long straddle has its maximum difference in price with the expiring short call. Similarly, the stock price at the strike price of the short put at expiration of the strangle is a point of maximum profit because the long put component of the long straddle has its maximum difference in price with the expiring short put. It is impossible to know for sure what the maximum profit potential is, because it depends on the price of the long straddle, and that price is subject to the level of volatility which can change.
Maximum risk
The maximum risk of a double diagonal spread is equal to the net cost of the spread including commissions. This amount is lost if the stock price is equal to the strike price of the straddle and if the straddle is held to its expiration. In this case, the value of the straddle declines to zero and the full amount paid for the spread is lost.
Breakeven stock price at expiration of the short call
There are two breakeven points, one above the strike price of the short call and one below the strike price of the short put. Conceptually, a breakeven point at expiration of the short strangle is the stock price at which the price of the long straddle equals the net cost of the spread minus the expiration value of the strangle. It is impossible to know for sure what the breakeven stock price will be, however, because it depends of the price of the long straddle which depends on the level of volatility.
Profit/Loss diagram and table: double diagonal spread
| Sell 1 28-day XYZ 95 put at | 1.30 |
| Buy 1 56-day XYZ 100 put at | (3.80) |
| Buy 1 56-day XYZ 100 call at | (4.00) |
| Sell 1 28-day XYZ 105 call at | 1.50 |
| Net cost = | (5.00) |
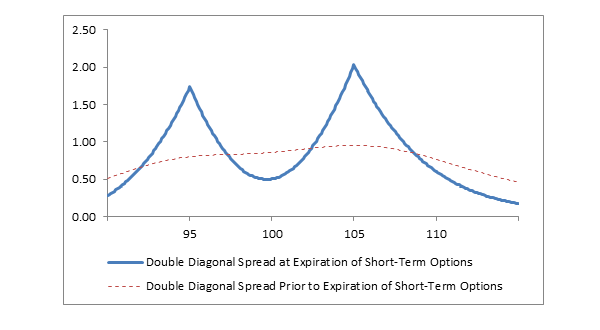
| Stock Price at Expiration of the 28-day Options | Short 1 28-day 95-105 Strangle Profit/(Loss) at Expiration | Long 1 56-day 100 Straddle Profit/(Loss) at Expiration of the 28-day Options* | Net Profit / (Loss) at Expiration of the 28-day Options |
|---|---|---|---|
| 120 | (12.20) | +12.15 | (0.05) |
| 115 | (7.20) | +7.65 | +0.45 |
| 110 | (2.20) | +3.00 | +0.80 |
| 105 | +2.80 | (1.85) | +0.95 |
| 100 | +2.80 | (1.90) | +0.90 |
| 95 | +2.80 | (1.95) | +0.85 |
| 90 | (2.20) | +2.70 | +0.50 |
| 85 | (12.20) | +12.15 | (0.05) |
*Profit or loss of the long straddle is based on its estimated value on the expiration date of the short strangle. This value was calculated using a standard Black-Scholes options pricing formula with the following assumptions: 28 days to expiration, volatility of 30%, interest rate of 1% and no dividend.
Appropriate market forecast
A double diagonal spread realizes its maximum profit if the stock price equals one of the strike prices of the short strangle on the expiration date of the short strangle. The forecast, therefore, must be “neutral.”
Typically, the stock price is at or near the strike price of the straddle when the position is established, and the forecast is for neutral price action between the strike prices of the short strangle.
Strategy discussion
A double diagonal spread is the strategy of choice when the forecast is for stock price action between the strike prices of the short strangle, because the strategy profits from time decay of the short strangle. Unlike a short strangle, however, a double diagonal spread has limited risk if the stock price rises or fall sharply beyond one of the strike prices of the short strangle. The tradeoff is that a double diagonal spread is established for a net debit and has a much lower profit potential than a short strangle. A double diagonal spread must also be closed at or prior to the expiration date of the strangle and, therefore involves more bid-ask spreads and commissions than a strangle.
Patience and trading discipline are required when trading double diagonal spreads. Patience is required because this strategy profits from time decay, and stock price action can be unsettling as it rises and falls around one of the strike prices of the short strangle as expiration approaches. Trading discipline is required because the profit potential of a double diagonal spread is “small” in dollar terms. Traders must, therefore, enter limit-price orders when entering and exiting a double diagonal spread position. Traders must also be disciplined in taking partial profits if possible and in taking “small” losses before the losses become “big.”
Impact of stock price change
“Delta” estimates how much a position will change in price as the stock price changes. Long calls and short puts have positive deltas, and long puts and short calls have negative deltas. If the stock price is close to the strike price of the straddle when a double diagonal spread is first established, the net delta is close to zero. With changes in stock price and passing time, however, the net delta varies from slightly positive to slightly negative, depending on the relationship of the stock price to the strike prices of the short options and on the time to expiration of the short strangle.
If the stock price equals the strike price of the short call at expiration of the short strangle, the position delta approaches +0.50. In this case, the delta of the in-the-money long call is approximately +0.75 (depending on volatility and on the time to expiration), and the delta of the out-of-the-money long put is approximately −0.25.
If the stock price equals the strike price of the short put at expiration of the short strangle, the position delta approaches −0.50. In this case, the delta of the in-the-money long put is approximately −0.75 (depending on volatility and on the time to expiration), and the delta of the out-of-the-money long call is approximately +0.25.
If the stock price is above the strike price of the short call at expiration of the short strangle, the position delta is negative, because the delta of the long call approaches +0.90 and the delta of the in-the-money expiring short call approaches −1.00. If the stock price is below the strike price of the short put at expiration of the short strangle, the position delta is positive, because the delta of the long put approaches −0.90 and the delta of the in-the-money expiring short put approaches +1.00.
Impact of change in volatility
Double diagonal spreads are highly sensitive to volatility. It is therefore necessary to forecast that volatility not fall when using this strategy.
Volatility is a measure of how much a stock price fluctuates in percentage terms, and volatility is a factor in option prices. As volatility rises, option prices tend to rise if other factors such as stock price and time to expiration remain constant. Long options, therefore, rise in price and make money when volatility rises, and short options rise in price and lose money when volatility rises. When volatility falls, the opposite happens; long options lose money and short options make money. “Vega” is a measure of how much changing volatility affects the net price of a position.
Since vegas decrease as expiration approaches, a double diagonal spread has a net positive vega. Consequently, rising volatility helps the position and falling volatility hurts. The vega is highest when the stock price is equal to the strike price of the long straddle and is only slightly lower when the stock price is equal to the one of the strike prices of the short strangle.
The net vega approaches zero if the stock price rises or falls sharply beyond one of the strike prices of the short strangle. At that point, one long option and one short option are both deep in the money, and the other options are far out of the money. The vegas of the out-of-the-money options are close to zero, and the vegas of the in-the-money options are approximately equal and opposite and, therefore, offsetting. Consequently, the net vega of the entire double diagonal spread is zero.
Impact of time
The time value portion of an option’s total price decreases as expiration approaches. This is known as time erosion. “Theta” is a measure of how much time erosion affects the net price of a position. Long option positions have negative theta, which means they lose money from time erosion, if other factors remain constant; and short options have positive theta, which means they make money from time erosion.
A double diagonal spread has a net positive theta as long as the stock price is in a range between the strike prices of the short strangle. This means that a double diagonal spread profits from time decay.
If the stock price rises or falls beyond a breakeven point, then the theta approaches zero. At such a stock price, however, a double diagonal spread has undoubtedly reached the point of maximum risk.
Risk of early assignment
Stock options in the United States can be exercised on any business day, and holders of short stock option positions have no control over when they will be required to fulfill the obligation. Therefore, the risk of early assignment is a real risk that must be considered when entering into positions involving short options.
While the long call and long put in a double diagonal spread have no risk of early assignment, the short call and put do have such risk. Early assignment of stock options is generally related to dividends. Short calls that are assigned early are generally assigned on the day before the ex-dividend date, and short puts that are assigned early are generally assigned on the ex-dividend date. In-the-money calls and puts whose time value is less than the dividend have a high likelihood of being assigned.
If the short call is assigned, then 100 shares of stock are sold short and the long call remains open. If a short stock position is not wanted, it can be closed in one of two ways. First, 100 shares can be purchased in the market place. Second, the short 100-share position can be closed by exercising the long call. Remember, however, that exercising a long call will forfeit the time value of that call. Therefore, it is generally preferable to buy shares to close the short stock position and then sell the long call. This two-part action recovers the time value of the long call. One caveat is commissions. Buying shares to cover the short stock position and then selling the long call is only advantageous if the commissions are less than the time value of the long call.
If the short put is assigned, then 100 shares of stock are purchased and the long put remains open. If a long stock position is not wanted, it can be closed in one of two ways. First, 100 shares can be sold in the marketplace. Second, the long 100-share position can be closed by exercising the long put. Remember, however, that exercising a long put will forfeit the time value of that put. Therefore, it is generally preferable to sell shares to close the long stock position and then sell the long put. This two-part action recovers the time value of the long put. One caveat is commissions. Selling shares to close the long stock position and then selling the long put is only advantageous if the commissions are less than the time value of the long put.
Note, however, that whichever method is used, trading stock or exercising a long option, the date of the stock purchase (or sale) will be one day later than the date of the short sale (or purchase). This difference will result in additional fees, including interest charges and commissions. Assignment of a short option might also trigger a margin call if there is not sufficient account equity to support the stock position created.
Potential position created at expiration of the short strangle
The position at expiration of the short strangle depends on the relationship of the stock price to the strike prices of the short options. If the stock price is at or between the strike prices of the short strangle, then the both short options expire worthless and the long straddle remains open.
If the stock price is above the strike price of the short call, however, then the short call is assigned. The result is a three-part position consisting of a long call, a long put and short 100 shares of stock. If the stock price is above the strike price of the short call immediately prior to its expiration, and if a position of short 100 shares is not wanted, then the short call must be closed.
If the stock price is below the strike price of the short put, then the short put is assigned. The result is a three-part position consisting of a long put, a long call and long 100 shares of stock. If the stock price is below the strike price of the short put immediately prior to its expiration, and if a position of long 100 shares is not wanted, then the short put must be closed.
Other considerations
Double diagonal spreads can be described in two ways. First, as described here, they are the combination of a longer-term straddle and a shorter-term strangle. Second, they can also be described as the combination of a diagonal spread with calls and a diagonal spread with puts in which the long call and long put have the same strike price.
The term “diagonal” in the strategy name originated when options prices were listed in newspapers in a tabular format. Strike prices were listed vertically in rows, and expirations were listed horizontally in columns. Therefore a “diagonal spread” involved options in different rows and different columns of the table; i.e., they had different strike prices and different expiration dates.
Note: This is an advanced strategy because the profit potential is small in dollar terms. As a result, it is essential to open and close the position at “good prices.” The commissions for four options, and potentially more options if some are exercised or assigned, could have a significant effect on the potential profit of this strategy.

