Potential goals
To profit from a bearish stock price move beyond the strike price of the long puts with limited risk if the stock price rises.
Explanation
A 1x2 ratio volatility spread with puts is created by selling one higher-strike put and buying two lower-strike puts. This strategy can be established for either a net credit (as seen in the example) or for a net debit, depending on the time to expiration, the percentage distance between the strike prices and the level of volatility. Profit potential is substantial and risk is limited, although the maximum risk is higher than the initial cost to establish the position. Profit is realized if the stock price falls sharply below the strike price of the long puts.
Example of 1x2 ratio volatility spread with puts
| Sell 1 XYZ 100 put at 3.50 |
| Buy 2 XYZ 95 puts at 1.50 each |
Maximum profit
On the downside, profit potential is substantial. The position has a long put, and the stock price can fall substantially.
On the upside, potential profit depends on whether the position is established for a net credit or net debit. If established for a net credit including commissions, then profit potential is limited to the net credit received. If the stock price is above the higher strike price at expiration, then all options expire worthless and the net credit is kept as a profit. If established for net debit, there is no profit on the upside; a loss equal to the net debit is incurred if all options expire worthless.
Maximum risk
Risk is limited and the maximum risk is realized if the stock price is at the strike price of the long puts at expiration. At the strike price of the long puts at expiration, the bull put spread is at its maximum value (and maximum loss) and the long puts expire worthless.
If the position is established for a net credit (amount received), the maximum risk equals the difference between the strike prices minus the net credit including commissions. In the example above, the maximum risk is 4.50, because the difference between the strike prices is 5.00 (100.00 – 95.00) and the net credit is 0.50. Therefore, 5.00 − 0.50 = 4.50.
If the position is established for a net debit (cost), the maximum risk is limited to the difference between the strike prices plus the net debit plus commissions. If the position had been established for net debit of 50 cents (0.50), the maximum risk would be 5.50, because the difference between the strike prices is 5.00 (100.00 – 95.00) and the net debit would have been 0.50. Therefore, 5.00 + 0.50 = 5.50.
Breakeven stock price at expiration
If the position is established for a net credit (as above), there are two breakeven points: Higher breakeven point: Higher strike price minus the net credit In this example: 100.00 − 0.50 = 99.50 Lower breakeven point: Lower strike price minus the maximum risk In this example: 95.00 − 4.50 = 90.50
If the position is established for a net debit, there is one breakeven point: Assuming the position was established for a net debit of 50 cents (0.50): Breakeven point: Lower strike price minus the maximum risk 95.00 − 5.50 = 89.50
Note: If this position is established for a net debit, there is no “higher breakeven point.” If the stock price is above the higher strike price at expiration, then all options expire worthless, and the net debit plus commissions is lost.
Profit/Loss diagram and table: 1x2 ratio volatility spread with puts
| Sell 1 XYZ 100 put at 3.50 |
| Buy 2 XYZ 95 puts at 1.50 each |
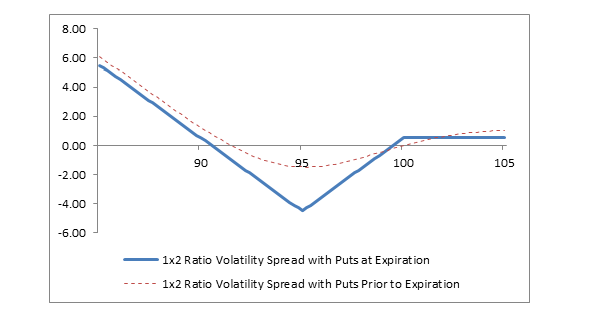
| Stock Price at Expiration | Short 1 100 Put Profit/(Loss) at Expiration | Long 2 95 Puts Profit/(Loss) at Expiration | Net Profit/(Loss) at Expiration |
|---|---|---|---|
| 103 | +3.50 | (3.00) | +0.50 |
| 102 | +3.50 | (3.00) | +0.50 |
| 101 | +3.50 | (3.00) | +0.50 |
| 100 | +3.50 | (3.00) | +0.50 |
| 99 | +2.50 | (3.00) | (0.50) |
| 98 | +1.50 | (3.00) | (1.50) |
| 97 | +0.50 | (3.00) | (2.50) |
| 96 | (0.50) | (3.00) | (3.50) |
| 95 | (1.50) | (3.00) | (4.50) |
| 94 | (2.50) | (1.00) | (3.50) |
| 93 | (3.50) | +1.00 | (2.50) |
| 92 | (4.50) | +3.00 | (1.50) |
| 91 | (5.50) | +5.00 | (0.50) |
| 90 | (6.50) | +7.00 | +0.50 |
| 89 | (7.50) | +9.00 | +1.50 |
| 88 | (8.50) | +11.00 | +2.50 |
| 87 | (9.50) | +13.00 | +3.50 |
Appropriate market forecast
A 1x2 ratio volatility spread with puts realizes its maximum profit if the stock price falls sharply below the strike price of the long puts. The forecast, therefore, must be “very bearish.” However, there must also be a reason for the desire to reduce risk if the stock price goes up instead of down. The forecast, therefore, must also include an element of high volatility. For example, consider a situation in which an earnings report or other company announcement is about to be made. A trader might forecast a bearish report and a sharply falling stock price. Nevertheless, the trader could also believe that the stock price will rise sharply if the news better than anticipated. A 1x2 ratio volatility spread with puts would profit if the forecast is correct and potentially risk little if the forecast is wrong. This strategy is sensitive to the level of volatility; see Impact of Change in Volatility below.
Strategy discussion
A 1x2 ratio volatility spread with puts is the same as selling a bull put spread and simultaneously buying a put with the same strike price as the long put in the bull put spread. The net premium received from the bull put spread is used to at least partially pay for the long put. The position profits if the underlying stock falls sharply beyond the strike price of the long puts.
The advantage of this strategy is than an out-of-the-money put is purchased for a “low” cost, or possibly a net credit. The disadvantages are (1) that risk is greater than the initial net cost and (2) that the breakeven point is further from the current stock price than an at-the-money long put.
A 1x2 ratio volatility spread with puts is very sensitive to changing volatility. A “small” decline in stock price accompanied by falling volatility might result in a loss, whereas an at-the-money long put might profit. It is therefore important to believe that “volatility is low” when establishing this strategy.
Impact of stock price change
“Delta” estimates how much a position will change in price as the stock price changes. Long puts have negative deltas, and short puts have positive deltas. The net delta of a 1x2 ratio volatility spread with puts varies from −1.00 to +1.00, depending on the relationship of the stock price to the strike prices of the options.
When established, the initial delta of a 1x2 ratio volatility spread with puts is negative. Furthermore, the delta falls (gets more negative) as the stock price falls and rises (gets less negative) as the stock price rises. In the language of options, this is known as a “positive gamma.”
As expiration approaches, the position delta approaches +1.00 if the short put is in the money and the long puts are out of the money. In this case, the delta of the short put approaches +1.00, and the deltas of the long puts approach zero.
When the stock price is below the strike price of the long puts as expiration approaches, the position delta approaches −1.00, because the delta of the short put approaches +1.00 and the deltas of the two long puts approach −1.00 each.
The position delta approaches zero as the stock price rises above the strike price of the short put, because the deltas of all puts approach zero.
Impact of change in volatility
Volatility is a measure of how much a stock price fluctuates in percentage terms, and volatility is a factor in option prices. As volatility rises, option prices tend to rise if other factors such as stock price and time to expiration remain constant. Long options, therefore, rise in price and make money when volatility rises, and short options rise in price and lose money when volatility rises. When volatility falls, the opposite happens; long options lose money and short options make money. “Vega” is a measure of how much a change in volatility affects the net price of a position.
In general a 1x2 ratio volatility spread with puts has a net positive vega, because the position has two long puts and one short put. However, the impact of changing volatility, i.e., the net vega, varies depending on the relationship of the stock price to the strike prices and on the time to expiration.
When first established, assuming the stock price is close to the strike price of the short put and there are 28 days or more to expiration, the net vega is positive, because the total positive vega of the two long puts is greater than the negative vega of the one short put.
As expiration approaches, if the stock price is close to or below the strike price of the long puts (lower strike), then the net vega is positive. If the stock price is close to the strike price of the short put (higher strike), then the net vega tends to be negative. The net vega approaches zero if the stock price rises above the higher strike.
Impact of time
The time value portion of an option’s total price decreases as expiration approaches. This is known as time erosion. “Theta” is a measure of how much time erosion affects the net price of a position. Long options have negative theta, which means they lose money from time erosion; and short options have positive theta and profit from time erosion, if other factors remain constant.
In general a 1x2 ratio volatility spread with puts has a net negative theta, because the position has two long puts and one short put. However, the impact of time erosion varies depending on the relationship of the stock price to the strike prices and on the time to expiration.
When first established, assuming the stock price is close to the strike price of the short put and there are 14 days or more to expiration, the net theta is negative, because the total negative theta of the two long puts is greater than the positive theta of the one short put. As a result, the position loses money from time decay.
As expiration approaches, if the stock price is close to or below the strike price of the long puts (lower strike), then the net theta is negative. If the stock price is close to the strike price of the short put (higher strike), then the net theta tends to be positive. The net theta approaches zero if the stock price rises above the higher strike.
Risk of early assignment
Stock options in the United States can be exercised on any business day, and holders of short stock option positions have no control over when they will be required to fulfill the obligation. Therefore, the risk of early assignment is a real risk that must be considered when entering into positions involving short options.
While the long puts in 1x2 ratio volatility spread with puts have no risk of early assignment, the short put does have such risk. Early assignment of stock options is generally related to dividends, and short puts that are assigned early are generally assigned on the ex-dividend date. In-the-money short puts whose time value is less than the dividend have a high likelihood of being assigned.
If assignment is deemed likely, there are two possibilities. First, the short put is assigned. In this case, 100 shares of stock are purchased and the two long puts remain open. Second, the put is not assigned. No matter how likely assignment may seem, there is no assurance that it will occur. In this case the 1x2 ratio volatility spread with puts remains intact.
If early assignment of the short put occurs, stock is purchased, and a stock position of long 100 shares is created. Assignment of the short put does not increase the maximum potential risk, because the long puts that limit position risk remain intact.
If early assignment of the short put does occur and if a long stock position is not wanted, the long stock position can be closed by either exercising one of the long puts and leaving the other put open or buy selling 100 shares in the marketplace and leaving both long puts open. Note, however, that whichever method is used, the date of the stock sale will be one day later than the date of the purchase (by assignment of the short put). This difference will result in additional fees, including interest charges and commissions. Assignment of a short put might also trigger a margin call if there is not sufficient account equity to support the long stock position.
Potential position created at expiration
The position at expiration depends on the relationship of the stock price to the strike prices. If the stock price is at or above the strike price of the short put (higher strike), then all options expire worthless and there is no stock position.
If the stock price is below the higher strike but not below the lower strike, then the short put is assigned and the long puts expire. Assignment of a short put causes stock to be purchased at the strike price, so the result is a long stock position. Since options are exercised at expiration if they are one cent (0.01) in the money, if a long stock position is not wanted, then the short put must be closed (purchased) prior to expiration.
If the stock price is below the lower strike price then the short put is assigned and both long puts are exercised. In the example above, this means that 100 shares are purchased and 200 shares are sold. The result is a net position of short 100 shares. If the stock price is below the lower strike immediately prior to expiration, and if a position of short 100 shares is not wanted, then one of the long puts must be sold.
Other considerations
In a “ratio spread” there is a difference between the number of options purchased and the number of options sold. The term “volatility” in the name of this strategy implies that more options are purchased than sold. In contrast, in the “1x2 ratio vertical spread with puts,” the term “vertical” implies that more options are sold than purchased.
This strategy – the 1x2 ratio volatility spread with puts – is also known as a “back spread,” because it is generally used with longer-term, or “back-month,” options as opposed to shorter-term, or “front-month,” options. Longer-term options are more suitable for this strategy, because this strategy profits mostly from stock price movement and is hurt by time decay. Longer-term options not only decay at a slower rate than shorter-term options, they also afford more time for the predicted stock price move to occur.
