Potential goals
To profit from a bullish stock price move beyond the strike price of the long calls with limited risk if the stock price falls.
A 1x2 ratio volatility spread with calls is created by selling one lower-strike call and buying two higher-strike calls. This strategy can be established for either a net credit (as seen in the example) or for a net debit, depending on the time to expiration, the percentage distance between the strike prices and the level of volatility. Profit potential is unlimited and risk is limited, although the maximum risk is higher than the initial cost to establish the position. Profit is realized if the stock price rises sharply above the strike price of the long calls.
Example of 1x2 ratio volatility spread with calls
| Sell 1 XYZ 100 call at 3.30 |
| Buy 2 XYZ 105 calls at 1.50 each |
On the upside, profit potential is unlimited, because the position has a long call, and the stock price can rise indefinitely.
On the downside, potential profit depends on whether the position is established for a net credit or net debit. If established for a net credit including commissions, then profit potential is limited to the net credit received. If the stock price is below the lower strike price at expiration, then all options expire worthless and the net credit is kept as a profit. If established for net debit, there is no profit on the downside; a loss equal to the net debit is incurred if all options expire worthless.
Risk is limited and the maximum is realized if the stock price is at the strike price of the long calls at expiration. At the strike price of the long calls at expiration, the bear call spread is at its maximum value (and maximum loss) and the long calls expire worthless.
If the position is established for a net credit (amount received), the maximum risk equals the difference between the strike prices minus the net credit including commissions. In the example above, the maximum risk is 4.70, because the difference between the strikes prices is 5.00 (105.00 - 100.00) and the net credit is 0.30. Therefore, 5.00 − 0.30 = 4.70.
If the position is established for a net debit (cost), the maximum risk is limited to the difference between the strike prices plus the net debit including commissions. If the position had been established for net debit of 50 cents (0.50), the maximum risk would be 5.50, because the difference between the strikes is 5.00 (105.00 - 100.00) and the net debit would have been 0.50. Therefore, 5.00 + 0.50 = 5.50.
If the position is established for a net credit (as above), there are two breakeven points: Lower breakeven point: Lower strike price plus the net credit In this example: 100.00 + 0.30 = 100.30 Higher breakeven point: Higher strike price plus the maximum risk In this example: 105.00 + 4.70 = 109.70
If the position is established for a net debit, there is one breakeven point: Assuming the position was established for a net debit of 50 cents (0.50): Breakeven point: Higher strike price plus the maximum risk 105.00 + 5.50 = 110.50
Note: If this position is established for a net debit, there is no “lower breakeven point.” If the stock price is below the lower strike price at expiration, then all options expire worthless, and the net debit plus commissions is lost.
| Sell 1 XYZ 100 call at 3.30 |
| Buy 2 XYZ 105 calls at 1.50 each |
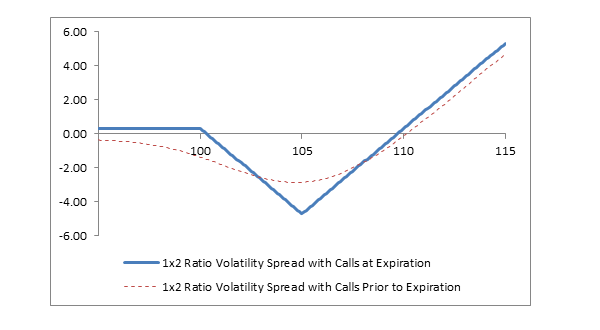
| Stock Price at Expiration | Short 1 100 Call Profit/(Loss) at Expiration | Long 2 105 Calls Profit/(Loss) at Expiration | Net Profit/(Loss) at Expiration |
|---|---|---|---|
| 113 | (9.70) | +13.00 | 3.30 |
| 112 | (8.70) | +11.00 | 2.30 |
| 111 | (7.70) | +9.00 | 1.30 |
| 110 | (6.70) | +7.00 | 0.30 |
| 109 | (5.70) | +5.00 | (0.70) |
| 108 | (4.70) | +3.00 | (1.70) |
| 107 | (3.70) | +1.00 | (2.70) |
| 106 | (2.70) | (1.00) | (3.70) |
| 105 | (1.70) | (3.00) | (4.70) |
| 104 | (0.70) | (3.00) | (3.70) |
| 103 | +0.30 | (3.00) | (2.70) |
| 102 | +1.30 | (3.00) | (1.70) |
| 101 | +2.30 | (3.00) | (0.70) |
| 100 | +3.30 | (3.00) | +0.30 |
| 99 | +3.30 | (3.00) | +0.30 |
| 98 | +3.30 | (3.00) | +0.30 |
| 97 | +3.30 | (3.00) | +0.30 |
A 1x2 ratio volatility spread with calls realizes its maximum profit if the stock price rises sharply above the strike price of the long calls. The forecast, therefore, must be “very bullish.” However, there must also be a reason for the desire to reduce risk if the stock price goes down instead of up. The forecast, therefore, must also include an element of high volatility. For example, consider a situation in which an earnings report or other company announcement is about to be made. A trader might forecast a bullish report and a sharply rising stock price. Nevertheless, the trader could also believe that the stock price will fall sharply if the news is not as good as anticipated. A 1x2 ratio volatility spread with calls would profit if the forecast is correct and potentially risk little if the forecast is wrong. This strategy is sensitive to the level of volatility; see Impact of Change in Volatility below.
A 1x2 ratio volatility spread with calls is the same as selling a bear call spread and simultaneously buying a call with the same strike price as the long call in the bear call spread. The net premium received from the bear call spread is used to at least partially pay for the long call. The position profits if the underlying stock rises sharply beyond the strike price of the long calls.
The advantage of this strategy is than an out-of-the-money call is purchased for a “low” cost, or possibly a net credit. The disadvantages are (1) that risk is greater than the initial net cost and (2) that the breakeven point is further from the current stock price than an at-the-money long call.
A 1x2 ratio volatility spread with calls is very sensitive to changing volatility. A “small” rise in stock price accompanied by falling volatility might result in a loss, whereas an at-the-money long call might profit. It is therefore important to believe that “volatility is low” when establishing this strategy.
“Delta” estimates how much a position will change in price as the stock price changes. Long calls have positive deltas, and short calls have negative deltas. The net delta of a 1x2 ratio volatility spread with calls varies from +1.00 to −1.00, depending on the relationship of the stock price to the strike prices of the options.
When established, the initial delta of a 1x2 ratio volatility spread with calls is positive. Furthermore, the delta rises as the stock price rises and falls as the stock price falls. In the language of options, this is known as a “positive gamma.”
As expiration approaches, the position delta approaches −1.00 if the short call is in the money and the long calls are out of the money. In this case, the delta of the short call approaches −1.00, and the deltas of the long calls approach zero.
When the stock price is above the strike price of the long calls as expiration approaches, the position delta approaches +1.00. In this case, the delta of the short call approaches −1.00 and the deltas of the two long calls approach +1.00 each.
The position delta approaches zero as the stock price falls below the strike price of the short call, because the deltas of all calls approach zero.
Volatility is a measure of how much a stock price fluctuates in percentage terms, and volatility is a factor in option prices. As volatility rises, option prices tend to rise if other factors such as stock price and time to expiration remain constant. Long options, therefore, rise in price and make money when volatility rises, and short options rise in price and lose money when volatility rises. When volatility falls, the opposite happens; long options lose money and short options make money. “Vega” is a measure of how much a change in volatility affects the net price of a position.
In general a 1x2 ratio volatility spread with calls has a net positive vega, because the position has two long calls and one short call. However, the impact of changing volatility, i.e., the net vega, varies depending on the relationship of the stock price to the strike prices and on the time to expiration.
When first established, assuming the stock price is close to the strike price of the short call and there are 28 days or more to expiration, the net vega is positive, because the total positive vega of the two long calls is greater than the negative vega of the one short call.
As expiration approaches, if the stock price is close to or above the strike price of the long calls (higher strike), then the net vega is positive. If the stock price is close to the strike price of the short call (lower strike), then the net vega tends to be negative. The net vega approaches zero if the stock price falls below the lower strike.
The time value portion of an option’s total price decreases as expiration approaches. This is known as time erosion. “Theta” is a measure of how much time erosion affects the net price of a position. Long options have negative theta, which means they lose money from time erosion; and short options have positive theta and profit from time erosion, if other factors remain constant.
In general a 1x2 ratio volatility spread with calls has a net negative theta, because the position has two long calls and one short call. However, the impact of time erosion varies depending on the relationship of the stock price to the strike prices and on the time to expiration.
When first established, assuming the stock price is at or above the strike price of the short call and there are 14 days or more to expiration, the net theta is negative, because the total negative theta of the two long calls is greater than the positive theta of the one short call. As a result, the position loses money from time decay.
As expiration approaches, if the stock price is close to or above the strike price of the long calls (higher strike), then the net theta is negative. If the stock price is close to the strike price of the short call (lower strike), then the net theta tends to be positive. The net theta approaches zero if the stock price falls below the lower strike.
Stock options in the United States can be exercised on any business day, and holders of short stock option positions have no control over when they will be required to fulfill the obligation. Therefore, the risk of early assignment is a real risk that must be considered when entering into positions involving short options.
While the long calls in a 1x2 ratio volatility spread with calls have no risk of early assignment, the short call does have such risk. Early assignment of stock options is generally related to dividends, and short calls that are assigned early are generally assigned on the day before the ex-dividend date. In-the-money short calls whose time value is less than the dividend have a high likelihood of being assigned.
If assignment is deemed likely, there are two possibilities. First, the short call is assigned. In this case, 100 shares of stock are sold short and the two long calls remain open. Second, the call is not assigned. No matter how likely assignment may seem, there is no assurance that it will occur. In this case the 1x2 ratio volatility spread with calls remains intact.
If early assignment of the short call occurs, stock is sold, and a short stock position of 100 shares is created. Assignment of the short call does not increase the maximum potential risk, because the long calls that limit position risk remain intact.
If early assignment of the short call does occur and if a short stock position is not wanted, the short stock position can be closed by either exercising one of the long calls, if they are in the money, and leaving the other call open or buy purchasing 100 shares in the marketplace and leaving both long calls open. Note, however, that whichever method is used, the date of the stock purchase will be one day later than the date of the short sale (by assignment of the short call). This difference will result in additional fees, including interest charges and commissions. Assignment of a short call might also trigger a margin call if there is not sufficient account equity to support the short stock position.
The position at expiration depends on the relationship of the stock price to the strike prices. If the stock price is at or below the strike price of the short call (lower strike), then all options expire worthless and there is no stock position.
If the stock price is above the lower strike but not above the higher strike, then the short call is assigned and the long calls expire. Assignment of a short call causes stock to be sold at the strike price, so the result is a short stock position. Since options are exercised at expiration if they are one cent (0.01) in the money, if a short-share position is not wanted, then the short call must be closed (purchased) prior to expiration.
If the stock price is above the higher strike price then the short call is assigned and both long are exercised. In the example above, this means that 100 shares are sold and 200 shares are purchased. The result is a net position of long 100 shares. If the stock price is above the higher strike immediately prior to expiration, and if a position of long 100 shares is not wanted, then one of the long calls must be sold.
In a “ratio spread” there is a difference between the number of options purchased and the number of options sold. The term “volatility” in the name of this strategy implies that more options are purchased than sold. In contrast, in the “1x2 ratio vertical spread with calls,” the term “vertical” implies that more options are sold than purchased.
This strategy – the 1x2 ratio volatility spread with calls – is also known as a “back spread,” because it is generally used with longer-term, or “back-month,” options, as opposed to shorter-term, or “front-month,” options. Longer-term options are more suitable for this strategy, because this strategy profits mostly from stock price movement and is hurt by time decay. Longer-term options not only decay at a slower rate than shorter-term options, they also afford more time for the predicted stock price move to occur.
